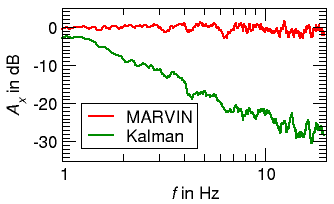
Die Aufgabe der Sensorauswertung ist die Interpretation der Sensordaten, um auf den Zustand des Hubschraubers zu schließen. Allgemein betrachtet soll der Zustand eines möglicherweise gesteuerten/geregelten Systems beobachtet werden. Üblicherweise gibt es aber bei der Messung des unbekannten Systemzustandes immer Störungen. Die Aufgabe, die Sensordaten aufzubereiten und ggf. zu fusionieren, um den wahren unbekannten Systemzustand möglichst genau zu schätzen, übernehmen spezielle Filteralgorithmen.

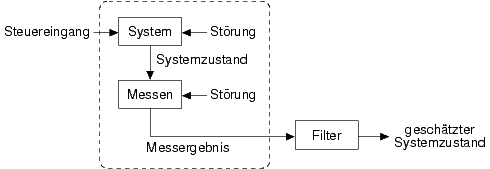
Ein weit verbreiteter Filteransatz sind Kalman-Filter, die es inzwischen in vielen verschiedenen Ausprägungen gibt. Im Internet gibt es viele Einführungsseiten zu dem Thema, wie z.B. die Seite von Greg Welch.

Ein Kalman-Filter besteht aus 2 Teilen:

• Der Vorhersageteil verfügt über ein Modellwissen des zu beobachtenden Systems. Er versucht, aus dem ungefähr bekannten Systemzustand die Veränderung des Zustandes vorherzusagen.
• Der Aktualisierungsteil vergleicht die gemessenen Sensorwerte mit denen aus der Vorhersage erwarteten. Mit Hilfe der bekannten Genauigkeit der Vorhersage und der Meßwerte wird nun eine neue wahrscheinlichste Schätzung berechnet.

Die Gundform des Kalman-Filters stellt die mathematisch beste Schätzung (minimierung der Unsicherheit des geschätzten Systemzustandes) für ein lineares System und ausschließlich Gaußschem Rauschen dar. Für nichtlineare System wie einen Hubschrauber muß der Algorithmus geeignet angepaßt werden. Das Erweiterte Kalman-Filter (engl. Extended Kalman Filter: EKF) linearisiert das Systemmodell im Punkt, der durch die gegenwärtige Schätzung bestimmt wird.

Zustandsvektor Für MARVIN wurde ein EKF entwickelt, das 15 Zustände (5 Vektorgrößen) schätzt:

• Position
• Geschwindigkeit
• Beschleunigung
• Orientierung
• Winkelgeschwindigkeit

Die Translationsbeschleunigung wurde als Zustand aufgenommen, weil es dem Hubschrauber nicht möglich ist, die beschleunigenden Kräfte instantan zu ändern. Die Servos benötigen etwas Zeit, um neue Stellungen zu erreichen, so daß sich auch die Beschleunigung des Hubschraubers stetig ändert.
Die Rotationsgeschwindigkeit des Hauptrotors wird nicht mit einem aufwendigen Filter geschätzt, da eine Drehgeschwindigkeit durch präzise Zeitmessungen innerhalb des Mikrocontrollers sehr genau direkt bestimmt werden kann.

Meßgrößenvektor
Für die Bestimmung des Zustandes werden 15 Sensorwerte erfaßt und vom Filter fusioniert:

• Differentielles GPS
  Das verwendete GPS ist in der Lage, mit 10 Hz Positionsdaten mit einer Standardabweichung von etwa 1 cm zu liefern. Geschwindigkeitsinformationen werden mit derselben Rate auf etwa 2 cm geliefert.
• Beschleunigung
  Die Meßrate der Beschleunigungssensoren ist hoch genug, um in jedem Regelzyklus (40 Hz) einen Wert zu liefern. Die Standardabweichung liegt bei etwa 0,1 m/s².
• Gyroskope
  Winkelgeschwindigkeiten werden ebenfalls mit hoher Rate gemessen und einer Genauigkeit von 1 °/s. Die Temperaturdrift wird separat vor dem Kalman-Filter kompensiert.
• Kompaß
  Ein Magnetkompaß mißt die Richtung des magnetischen Feldes. Das Rauschen der Einheitsvektorkomponenten der Feldlinienrichtung beträgt dabei 0,075. Da ein Hubschrauber magnetische und magnetisierbare Metallteile enthält, ist eine Kompensation notwendig, die in zwei Stufen arbeitet. Die erste kompensiert unveränderliche überlagerte Magnetfelder, während sich die zweite um veränderliche orientierungsabhängige Ummagnetisierungen kümmert.
  Die Abweichung von magnetischem und geographischem Nordpol wird vom Kalman-Filter berücksichtigt.

Das Modell
Das Modell für die Vorhersage besteht aus den vollständigen Bewegungsgleichung für einen starren Körper. Desweiteren werden die erwarteten Bewegungen durch die Steuersignale berücksichtigt. Das aerodynamische Modell des Hubschraubers ist also dasselbe vereinfachte, das auch für die Regelung verwendet wird.

Das umfangreiche EKF wurde in der Simulation mit dem aktuell eingesetzten Filteralgorithmus MARVINs verglichen. Echte Flugtests wurden bisher nicht durchgeführt. Dies hat im wesentlichen zwei Gründe: Der verwendete Mikrocontroller besitzt keine FPU und die Rechenleistung reicht bei weitem nicht aus, um den EKF in Echtzeit im Flug zu berechnen. Außerdem kann die Abweichung zum exakten richtigen Zustand nur in der Simulation bestimmt werden, da in der Realität immer nur die fehlerbehafteten Sensorsignale vorliegen. Für eine Untersuchung der Ergebnisqualität bietet sich die Simulation also an.

Das implementierte EKF benötigt trotz einiger Laufzeitoptimierungen auf einem Pentium 5 mit 2,8 GHz 890 μs gegenüber nur 4,5 μs des Algorithmus' von MARVIN, also etwa 200 mal länger. Auf dem Mikrocontroller wäre das Verhältnis wegen der fehlenden FPU um einiges größer. Die absolute Genauigkeit der Ergebnisse für Position und Winkel ist kaum besser. Beschleunigung und Winkelgeschwindigkeiten werden mit etwa der halben absoluten Abweichung geschätzt. Anzumerken ist außerdem, daß in diesen Simulationen das Sensorrauschen exakt dem durch das EKF erwarteten entspricht, was in der Realität sicher nicht der Fall wäre.
Ein signifikanter Unterschied zwischen beiden Algorithmen ist die deutlich bessere Unterdrückung von hochfrequenten Meßfehlern durch das EKF (siehe Abbildung). Für die Flugregelung macht sich das aber nur wenig bemerkbar, da die Regelstrecke ohnehin als Tiefpaß wirkt.

Da das Kalman-Filter mit MARVINs gegenwärtiger Lagesensorik verglichen wurde, soll letztere hier kurz beschrieben werden.

Translatorischer Zustand
Für translatorische Bewegungen werden die GPS-Daten wegen deren hohen Genauigkeit direkt verwendet. Das bedeutet, wenn eine neue Positionsmessung erfolgt ist, wird diese direkt ohne Filterung übernommen. In Regelungszyklen, in denen keine neue GPS Messung zur Verfügung steht, wird die Position mittels der zuletzt gemessenen Geschwindigkeit extrapoliert.

Orientierung
Die Winkelgeschwindigkeiten werden direkt aus den driftkorrigierten Gyroskopen übernommen. Die Winkel werden prinzipiell ebenfalls aus diesen Werten integriert. Da hierbei aber unweigerlich Fehler entstehen, die schon nach kurzer Zeit zu sehr großen Abweichungen führen würden, erfolgt eine Korrektur mit Hilfe der übrigen Sensoren.

Die Orientierung wird intern durch einen Vektor nach Norden und einen nach unten repräsentiert. Norden kann dabei aus dem Kompaß bestimmt werden. Der Gravitationsvektor ist etwas aufwendiger. Da Bewegungsbeschleunigung prinzipbedingt nicht von Gravitationsbeschleunigung unterscheidbar ist (Äquivalenzprinzip), müssen die Werte der Beschleunigungssensoren, die die Summe beider Beschleunigungen messen, korrigiert werden. Die Bewegung kann aus den GPS-Informationen bestimmt werden, so daß diese Bewegungsbeschleunigung von der gemessenen Summe subtrahiert werden kann. Zu beachten ist dabei zusätzlich, daß die Bewegungsbeschleunigung aus den GPS-Daten signifikant älter sind als die der Beschleunigungssensoren.