• Die Auftriebskraft L (engl. lift) steht senkrecht zur Anströmenden Luft.
• Die Widerstandskraft D (engl. drag) ist parallel zur Anströmung.

• L=½ C_l ρ b l v²
• D=½ C_d ρ b l v²

Die Aufgabe des Modells ist die Berechnung des Flugverhaltens unter Berücksichtigung der Steuergrößen. Die oben eingeführten Pitch-Werte und die Gasstellung bilden also die Eingänge für das Modell. Die Zustandsgrößen des Hubschraubers sind die Ausgänge:

Insgesamt berücksichtigt das Modell deutlich mehr Zustandsvariablen als dargestellt:

• Position, Geschwindigkeit
• Orientierung, Rotationsgeschwindigkeit
• Rotationsgeschwindigkeit der Rotoren
• Kollektive und zyklische Pitch-Stellung des Hauptrotors (wegen Stellgrößenbeschränkungen sind diese nicht gleich den logischen Werten
• Heckrotorpitch, Kreiselintegrator (für den Fall eines Heckkreisels mit PI-Regler)
• Gasstellung

Das dargestellte Modell bildet alle Komponenten des Hubschraubers ab, die einen relevanten Einfluß auf das Flugverhalten haben.

Aktuatoren
Die erste Stufe, die die Steuersignale passieren, sind die Aktuatoren. Diese setzen die logischen Steuersignale in mechanische Bewegung um. Im Modellbau übernehmen Servos diese Aufgabe und verändern über eine geeignete Mechanik die Pitch-Winkel der Rotorblätter.
Für den Heckrotor wird üblicherweise noch ein Kreisel vor den Servo geschaltet, der den Gierwinkel des Hubschraubers stabilisiert. Ohne diesen Kreisel ist der Heckpitch-Steuereingang proportional zur Winkelbeschleunigung, mit Kreisel zur Winkelgeschwindigkeit. Die Implementierung des Modells bietet beide Varianten und zusätzlich die Wahl zwischen einem einfachen Kreisel (P-Regler) oder einen sogenannten Heading-Hold Kreisel, auch Heading-Lock genannt (PI-Regler).

Aerodynamik der Rotoren
Im Fall der Rotoren folgt nun als nächste Stufe die Berechnung des aerodynamischen Modells. Dies ist der aufwendigste Teil des Modells und wird auf einer eigenen Seite beschrieben.

Motor
Für den Motor wird zur Berechnung des Drehmoments die übliche Kennlinie herangezogen (siehe Abbildung mit Motordrehzahl n, Leistung P, Drehmoment M, hier für MARVINs Motor). Zusätzlich wird der Leistungsverlust durch eine veränderliche Luftdichte mittels der barometrischen Höhenformel und die Stellung des Gas-Servos beachtet.

Starrer Körper
Die Bewegungsgleichungen der starren Körper am Hubschrauber bestimmen die Bewegung, die aus den berechneten Kräften und Drehmomenten resultiert. Details folgen unten.

Insgesamt ergibt sich also ein Modell aus allen genannten Komponenten. Anzumerken ist noch, daß die einzelnen Blöcke weder in der Realität noch im vollständigen Modell komplett entkoppelt sind wie hier dargestellt:

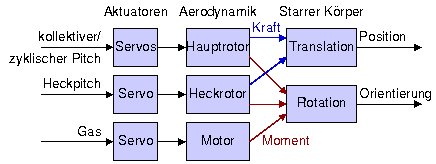
Das Modell der starren Körper im Hubschrauber basiert auf den üblichen Newtonschen Gesetzen.
Die Translatorische Bewegung kann leicht aus der bekannten Vektorgleichung berechnet werden:

• F = m a

F ist die (noch zu berechnende) angreifende Kraft, m die Hubschraubermasse und a die resultirende Beschleunigung. Dieser Ansatz gilt allerdings in dieser Form nur, wenn man die Bewegung des Schwerpunkts betrachtet. Liegt der Bezugspunkt des Hubschraubers nicht im Schwerpunkt, so ist zusätzlich die Rotationsbewegung des Hubschraubers zu beachten.

Zur Berechnung der Rotationsbewegung wird die nicht ganz so bekannte Euler-Gleichung der Mechanik benötigt. Sie beschreibt die Drehimpulserhaltung aus einem hubschrauberfesten, also mitgedrehten, Koordinatensystem heraus:

• M = dL/dt + ω x L

M ist das (noch zu berechnende) angreifende Drehmoment, L der Drehimpuls und ω die Rotationsgeschwindigkeit des Hubschraubers. Auch dies ist eine Vektorgleichung, die auf der rechten Seite zwei Terme besitzt, die zeitliche Ableitung des Drehimpulses sowie ein Kreuzprodukt aus der aktuellen Rotation und dem Drehimpuls. Dieses Kreuzprodukt ist für die bekannte 90°-Verschiebung zwischen angreifenden Moment und Neigerichtung des Hubschraubers verantwortlich. Diese Bewegung heißt Kreiselpräzession.
L setzt sich aus den Drehimpulsen der Rotoren (Trägheitstensor J_r), des Motors und des sich drehenden Rumpfes (Trägheitstensor J_h) zusammen. Mit der Rotationsgeschwindigkeit ω_r des Rotors ergibt sich als Gesamtgleichung:

• M = J_h . dω/dt + J_r . dω_r/dt + ω x (J_h . ω + J_r . ω_r)

Mit dieser Gleichung läßt sich nun die Veränderung der Rotationsbewegung unter den bekannten gegenwärtigen Bedingungen berechnen. Allerdings sind dies nur 3 skalare Gleichungen für 4 unbekannte Rotationsbeschleunigungen dω_h/dt und dω_r/dt (letztere weist im hubschrauberfesten Koordinatensystem immer in dieselbe Richtung, so daß die Vektorrichtung bekannt ist).

Es wird also noch eine weitere Gleichung benötigt, die den Einfluß des Motors auf die Drehzahl der Rotoren beschreibt. Sie kann als einfache Bilazgleichung aufgestellt werden. Mit M_m als Drehmoment vom Motor und M_r als Reibung vom Rotor ergibt sich damit:

• M_m - M_r = J_r dω_r/dt

Kräfte
Die Gesamtkraft F, die oben in der Gleichung für die Bewegung des starren Körpers benutzt wird, setzt sich aus mehreren Komponenten zusammen:

• Aerodynamische Kräfte der Rotoren
• Aerodynamische Widerstandskraft des Rumpfes im Wind oder bei Flugbewegungen
• Gewichtskraft

Momente
Die Summe M aller Drehmomente, die auf den Hubschrauber wirken, ergibt sich ebenfalls aus einer Reihe von Einzelmomenten:

• Luftwiderstand der Rotoren
• Steuermomente der Rotoren durch zyklischen Pitch oder unsymmetrische Anströmung
• Nicht im Schwerpunkt angreifende Kräfte der Rotoren
• Nicht im Schwerpunkt angreifende aerodynamische Widerstandskraft des Rumpfes

All diese Kräfte und Momente werden im Modell berücksichtigt und berechnet. Die aerodynamischen Kräfte und Momente der Rotoren werden auf einer eigenen Seite beschrieben.